Un polynôme à une seule variable est la somme d'un multiple constant d'une variable portée à différents exposants. Par exemple, 1 + x est un polynôme du premier ordre le plus élevé à cause de l'exposant x est égal à 1. 2 + 3x + x ^ 3 est un polynôme de troisième ordre. Les zéros (ou les racines d'un polynôme) sont les valeurs de x, où le polynôme est égale à zéro. Les zéros de second ordre et polynômes inférieurs peuvent être résolus par la main en utilisant la formule quadratique. Ordre supérieur polynômes ont généralement besoin d'être résolus avec des méthodes approximatives en utilisant un ordinateur.
Instructions
Manuellement
1 Mettez le polynôme sous la forme ax ^ 2 + bx + c, si le polynôme est de second ordre.
Dans ce cas, a, b et c sont des constantes, et x est une variable. (Notez que si a = 0, le polynôme est de premier ordre, qui est, juste une équation linéaire et peut être résolu par la main avec des manipulations arithmétiques de base. En d'autres termes, bx + c = 0 donne bx = -c, ou x = -c / b.)
2 Utilisez la formule quadratique à résoudre pour les zéros.
La formule quadratique est x = [-b +/- √ (b ^ 2 - 4ac)] / [2a], qui est la solution à la hache de l'équation ^ 2 + bx + c = 0. (Ceci peut être prouvé en utilisant la méthode de l'achèvement des carrés ou en insérant la solution dans la formule pour voir qu'il est vrai.)
+/- Signifie ici "plus ou moins." Si b ^ 2 - 4ac est pas égal à zéro, l'équation ci-dessus donne deux zéros. (Notez que les polynômes d'ordre n-ièmes ont n zéros.)
3 Utilisez i pour représenter √ (-1), si b ^ 2 - 4ac <0.
Cela donnera des nombres complexes comme les zéros de ax ^ 2 + bx + c. Les nombres complexes sont des nombres qui incluent le nombre imaginaire i. Dans le plan xy, la courbe de ax ^ 2 + bx + c ne pas toucher l'axe x à une valeur quelconque pour x. Par conséquent, certains livres de mathématiques rejettent la réponse dénuée de sens. Cependant, la définition de la racine carrée d'un nombre négatif comme le produit de i fois la racine carrée de la valeur absolue du nombre contourne cet obstacle.
Par exemple, √ (-100) = √ (-1) --- √100 = i --- 10 = 10i.
Par ordinateur: Bisection Méthode
4 Déterminer deux valeurs x proches du zéro prévue du polynôme P (x), de telle sorte que le polynôme est de signe opposé aux deux points.
Autrement dit, les deux valeurs x1 et x2 doit être telle que le signe (P (x1)) = - connexion (P (x2)).
Par conséquent, les deux valeurs de x seront liés au zéro, et P (x1) et P (x 2) seront au-dessus et au-dessous de l'axe x, délimitant l'axe x.
5 Calculer le point médian entre x1 et x2.
En d'autres termes, définir x3 = (x1 + x2) / 2.
6 Déterminer le signe du polynôme à x3, qui est, le signe de P (x3).
7 Jeter la valeur x qui donne le même signe que x3.
Par exemple, si X1 et X3 donnent le même signe pour P (x), jeter x1.
8 Calculer le point milieu des deux valeurs de x restantes, comme cela a été fait à l'étape 2.
9 Continuez à répéter les étapes 3-5 jusqu'à ce que P (x) est plus proche de zéro que une certaine tolérance, où x est l'approximation de la racine dans cette région.
X qui pousse la valeur absolue de P (x) au-dessous de ce niveau de tolérance, par exemple, 0,001, est l'approximation numérique du zéro pour la P (x). En d'autres termes, un X a été trouvé tel que | P (x) - 0 | <Niveau de tolérance.
dix Ensuite, répétez le processus ci-dessus, à partir de l'étape 1 à nouveau, pour trouver tous les autres zéros de P (x).
(Notez que les polynômes d'ordre n-ièmes ont n zéros.)
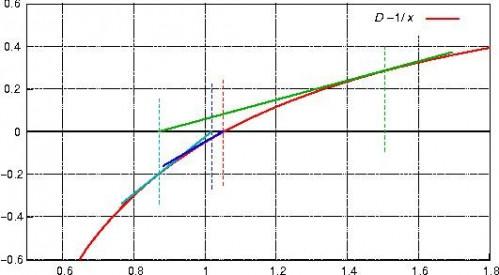
Par ordinateur: Newton-Raphson
Résoudre pour la dérivée du polynôme P (x).
Le monôme de la forme c --- x ^ n, où c et n sont des constantes, a dérivé cn --- x ^ (n-1). La dérivée d'un polynôme est la somme des dérivées des monômes. La dérivée d'une constante par lui-même est égal à zéro, étant donné que le graphique d'une constante est plat, qui est, ne variant pas avec x. Ainsi, par exemple, le dérivé de P (x) = 2x ^ 2 + 3 est p` (x) = 4x. (Notez la marque par le P indiquant le dérivé.)
12 Faire une meilleure estimation pour le zéro du polynôme, juste pour avoir un point de départ. Appelez x1.
13 Résolvez x2 = x1 - P (x1) / p` (x1).
14 Répétez l'étape 3 pour produire à partir x3 x2, x4 de x3, et ainsi de suite.
15 Arrêter l'itération (répétition de l'étape 3) après un X a été constaté que les lieux P (x) aussi proche de zéro si besoin.
Conseils et avertissements
- Les fonctions f (x) dont les racines ou les zéros, sont trouvées n'a pas besoin d'être polynômes. Les deux méthodes numériques (calcul) ci-dessus ne reposent pas sur les fonctions étant polynômes et peuvent être appliquées de façon plus générale.
- La méthode de Newton-Raphson est cependant pas généralisable à toutes les fonctions. La fonction doit être différentiables. Alors, pourquoi l'utiliser du tout? Parce qu'il converge vers zéro plus rapidement que la méthode de dichotomie, si la fonction est dérivable.