La méthode de Monte Carlo est une méthode de simulation à l'aide d'un grand ensemble de nombres aléatoires. Si la distribution de probabilité cumulative d'une population est connue, alors l'ensemble de nombres aléatoires peut être utilisé pour simuler la distribution, pour générer une population d'échantillon simulé. Pourquoi ne pas utiliser les données d'origine directement? Les raisons peuvent varier de l'accès aux données, au nombre insuffisant de points de données brutes pour la mesure de petits effets, à l'effort nécessaire pour préparer les données brutes, à une capacité supérieure à manipuler mathématiquement des données simulées.
Définitions
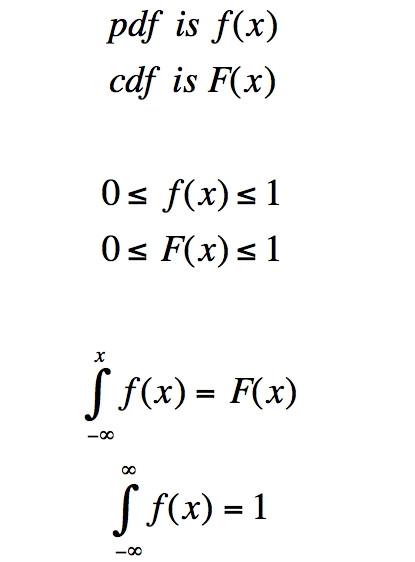
fonctions de densité de probabilité, ou pdfs, sont des fonctions avec la propriété que l'aire sous les résume à 1. La zone entre X = a et X = b est égale à la probabilité que X aura une valeur se situe entre a et b. Une fonction de distribution cumulative (cdf) pour un pdf particulier prend la valeur à X = x de la zone sous le pdf ci-dessous x. Notez que l'intégrale, du calcul, est la zone sous une fonction. Par conséquent, la cdf. d'un pdf est l'intégrale de la pdf de X = -∞ à X = x. Comme x se déplace vers le haut de -∞ à + ∞, la valeur cdf monte entre 0 et 1.
Exemples
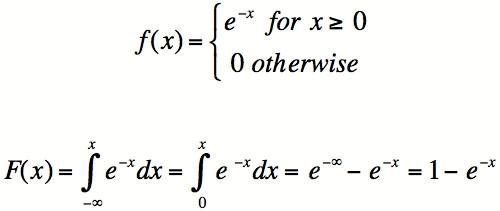
La probabilité que X est égal à x peut être égal à zéro. Ainsi, un pdf n'a pas besoin d'avoir un espace pour toutes les gammes entre -∞ et + ∞. Par exemple, un pdf pour un tirage au sort a la probabilité que deux valeurs: 1 tête, ou 0 têtes. La valeur de pdf pour chaque cours est de 0,5. Le cdf à X = 0 est de 0,5, étant donné que les valeurs de X jusqu'à et y compris 0 têtes ont une probabilité de 0,5. Le cdf à X = 1 est 1. Ceci est un exemple d'un pdf discret.
Un exemple moins trivial est une fonction exponentielle. La fdp continue f (x) = e -x ^ de 0 à + ∞ et 0 pour x négative a une superficie égale à 1. La probabilité que X est compris entre 1 et 2 est, par intégration, e ^ (- 1) - e ^ (- 2) ≈ 0,2325.
La base de simulations Monte Carlo
Si vous avez accès à un générateur de nombres aléatoires (par exemple, la fonction RAND dans Microsoft Excel), vous pouvez générer des nombres X qui ont la distribution d'un pdf donné. La façon de le faire est que le générateur variable aléatoire est de retour d'un nombre aléatoire entre 0 et 1. Le cdf est réglé sur cette valeur et X est résolu pour. Rappelez-vous, les gammes cdf de 0 à 1 seulement.
Un exemple de l'assurance
Supposons que l'on sait que la gravité des dommages à la propriété (PD) et des lésions corporelles (BI) revendique pour l'assurance automobile ont cdfs P (x) et B (y). Supposons également que la franchise est applicable à PD et BI combinés. Supposons également que l'effet que les différentes franchises auront sur la prime doit être calculée. Ensuite, pour simuler un grand nombre de revendications, de nombreuses variables aléatoires entre 0 et 1 peuvent être générés et mis à P (x) et B (y). X et Y peuvent alors être résolus et ajoutés de telle sorte qu'une déduction peut être appliquée. Ensuite, trouver le montant des différentes franchises d'intérêt de supprimer le montant de la perte x + y. Un total cumulé des pertes et des pertes éliminés alors donner les informations nécessaires pour calculer les facteurs d'actualisation déductibles.
Bien sûr, les numéros séparés seraient fixés à P (x) et B (y); autrement, une corrélation extrême et irréaliste serait construit dans les simulations. Idéalement, la cdf commune (une seule cdf qui décrit la distribution des deux variables ensemble) serait connu, pour tenir compte de la dépendance entre les PD et BI. Au minimum, la dépendance serait testé dans les données empiriques pour voir dans quelle mesure la corrélation existe.
A déterministes Exemple
Ce qui précède est une application probabiliste des simulations de Monte Carlo. Une application déterministe commune de Monte Carlo est simulations de particules qui obéissent à des équations aux dérivées partielles (EDP). Par exemple, il faudra peut être simulé de telle sorte qu'ils obéissent aux équations de la physique des plasmas pertinents (par exemple de Navier-Stokes) les électrons et les protons dans un réacteur de fusion. Variables aléatoires seraient utilisées pour simuler le risque de collision entre les particules spécifiques, tout en obéissant à des équations électromagnétiques générales qui ne sont pas faciles à résoudre pour une forme particulière du réacteur sans une simulation par ordinateur.
L'idée générale de déterministes simulations de Monte Carlo est que les équations générales peuvent être trop générale pour être facilement appliquée à des situations physiques très spécifiques. Les simulations à l'aide de variables aléatoires peuvent être faites comme des expériences virtuelles. L'avantage supplémentaire est que la manipulation est plus facile (par exemple, la forme du réacteur et des configurations magnétiques peuvent varier plus rapidement que dans un vrai réacteur expérimental.) Dans une expérience réelle, les outils de diagnostic peuvent interférer avec le système mesuré. Dans une simulation, cette question est supprimée, étant réduite à un exercice de calcul.