Comme les calculs mathématiques deviennent plus complexes, les équations deviennent plus lourdes. notation Scalar désigne seulement l'ampleur, tandis qu'un vecteur représente une grandeur et une direction. En mathématiques plus avancées, les scientifiques et les ingénieurs utilisent tenseurs pour la notation. Un tenseur représente une amplitude et deux ou plusieurs directions, ce qui inclut les entités scalaire et vectoriel. Un ordre zéro tenseur est un scalaire, un tenseur de premier ordre est un vecteur et un tenseur du second ordre est une matrice.
Notation

Un second ordre tenseur général utilise une variable avec trois indice, qui sont généralement "i", "j" et "k". Certains physique de pointe ou d'autres applications scientifiques plus élevées peuvent nécessiter des tenseurs ci-dessus second ordre, mais la plupart des applications ne nécessitent un second ordre ou au-dessous. Chaque indice représente le nombre de dimensions, ce qui est habituellement trois. Un ordre zéro tenseur n'a pas d'indices, une première commande a un et un second ordre a deux. Cette tendance se poursuit dans les tenseurs d'ordre supérieur.
Kronecker Delta
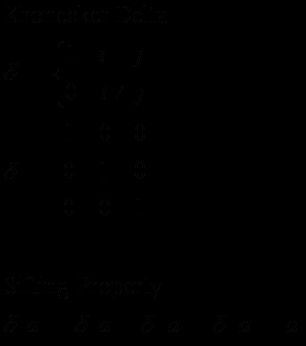
Le delta Kronecker est tenseur spécial qui représente la matrice d'identité. Le tenseur un égal quand "i" est égal à "j", mais il est nul lorsque "i" ne correspond pas à "j". Ce tenseur spécial a également un "criblage" la propriété, de sorte qu'un (i) donne un (j). Seuls les termes où "i" est égal à "j" sont affichés dans le graphique puisque les autres termes sont tous nuls par définition.
Vector Dot Product

Pour être utile, un tenseur doit faire plus que simplement représenter une certaine quantité - il doit aussi être capable de représenter un calcul. Une opération mathématique commune est le produit scalaire du vecteur, ou le produit intérieur. Cette opération vient d'une dérivation impliquant le delta Kronecker. Le graphique illustre deux deltas Kronecker étant multipliés ensemble. La dernière ligne de cette équation correspond à la définition d'un produit vecteur de points, donc une notation tenseur représente utilement un produit vecteur de points.
Alternant Tensor

Le tenseur alternatif est un autre tenseur spécial conçu pour faire certaines opérations mathématiques possibles. Comme le delta Kronecker, la valeur du tenseur alternatif est conditionnel à ses indices, mais où le delta Kronecker a deux indices, le tenseur alternatif a trois. Les valeurs nulles permettent une opération transversale du produit lorsqu'il est combiné avec deux tenseurs de premier ordre.
Symétrie

Un tenseur symétrique est celle dans laquelle t (i, j) = t (j, i). Un tenseur antisymétrique, dans lequel t (i, j) = t (j, i). N'importe quel tenseur peut être exprimée comme une moitié de la somme d'un tenseur symétrique et un tenseur antisymétrique. En trois dimensions (cartésien) l'espace, tout vecteur peut être transformé en un tenseur antisymétrique en utilisant le vecteur alternatif. Dans le graphique, oméga (k) est le vecteur et R (i, j) est le tenseur.